この図は「三次元 円筒座標 散布図(Three-dimensional Cylindrical Polar Scatter Graph)」と呼ばれるグラフの一例です。円筒座標系を用いて、極角・半径・高さという三つの値の関係を可視化しています。
一般的な散布図が二次元平面上に点をプロットするのに対し、この図では「角度(θ)」「半径(r)」「高さ(z)」の三要素を組み合わせることで、三次元的な分布を表現します。
これは極座標プロット(Polar Plot)の三次元拡張とみなすことができます。二次元の極座標散布図では平面上の角度と距離で表現しますが、さらに高さ軸を加えることで、データの変化をより立体的に理解できます。
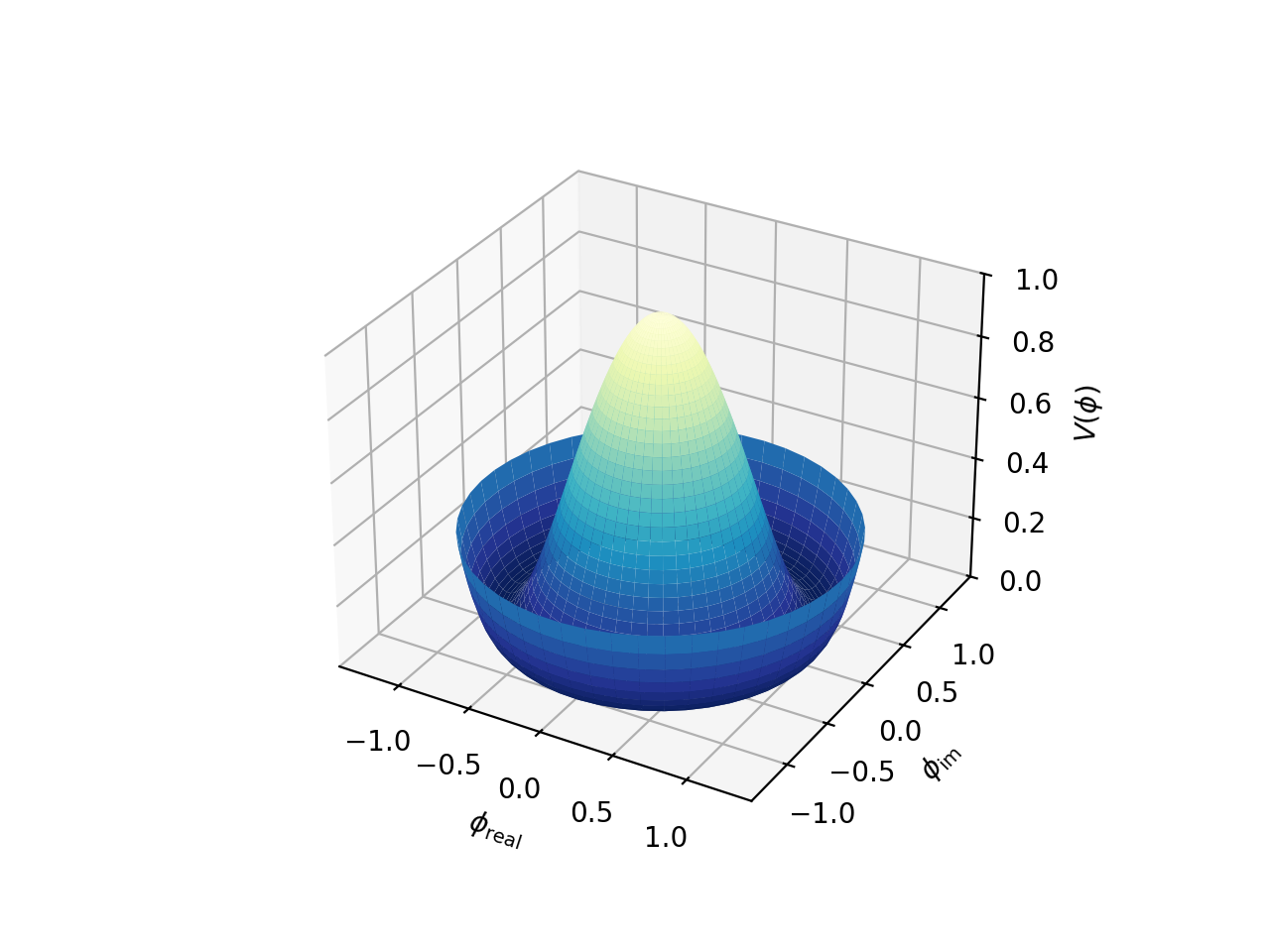

チャートの見方
- 底面(水平の円):角度方向(0°〜360°)と半径方向(0〜10)の二軸を表します。0°、30°、60°、…といった目盛りは、円周上の角度(極角θ)を示しています。
- 垂直軸(高さ方向):数値(ここでは0〜25)を表し、縦方向の値(z軸)として機能します。
- 黒い点(データポイント):各データの位置を示します。点の位置は、
- 角度(θ) … 円周上の方向
- 半径(r) … 中心からの距離
- 高さ(z) … 垂直方向の値
によって決定されます。
- 縦線(ドロップライン):データ点と底面を結ぶ線で、点の高さを明確にする補助線です。
このように、データを「方向」「距離」「高さ」という三つの変数で表すため、気象学・地球科学・工学など、周期性や角度を含む多変量データの分析によく用いられます。
目的と利用分野
三次元円筒座標散布図は、「角度」「距離」「高さ」という三つの変数を同時に可視化できるグラフです。主に次のような目的で利用されます。
1. 方向性をもつデータの分析
角度(0°〜360°)を用いることで 方位や方向をもつデータ を扱えます。たとえば次のような分野です。
| 分野 | 具体例 | 解釈のポイント |
|---|---|---|
| 気象学 | 風向・風速・高度 | 風がどの方向からどのくらいの強さで吹いているか |
| 海洋学 | 潮流の方向・深さ | 各深度での潮流方向の変化 |
| 通信工学 | アンテナの方向特性 | 角度ごとの信号強度(ゲイン)を立体的に表示 |
2. 周期的な現象の可視化
360°の角度を時間や周期に見立て 周期的な変化 を表すことができます。
- 例:1日を360°に見立てて、時刻ごとの温度や電力消費量をプロット
- 例:1年を円周に割り当て、月ごとの降水量や日照時間を高さで表現
このように「円周上の繰り返し」と「高さ方向の変化」を同時に見ることで、周期的パターンを一目で把握できます。
3. 三変数の同時比較
一般的な散布図では2軸(x, y)でしか関係を示せませんが、
円筒座標では次のように3軸を対応づけることができます。
| 軸 | 意味 | 例 |
|---|---|---|
| 角度(θ) | カテゴリ・方向・時間 | 方位・時間・角度 |
| 半径(r) | 距離・大きさ | 測定点までの距離、周波数など |
| 高さ(z) | 量的変数 | 強度、頻度、値の大きさなど |
これにより 3つの連続変数の関係性やパターン を立体的に把握できます。
4. 視覚的なプレゼンテーション
立体的な形状が特徴的なため 研究発表・学会ポスター・技術報告書 などでも利用されます。
特に、通常の平面グラフでは伝わりにくい「方向+強度+高さ」の関係を視覚的に表現できるため、観察的データの探索(exploratory data analysis)にも適しています。
背景と数理的基盤
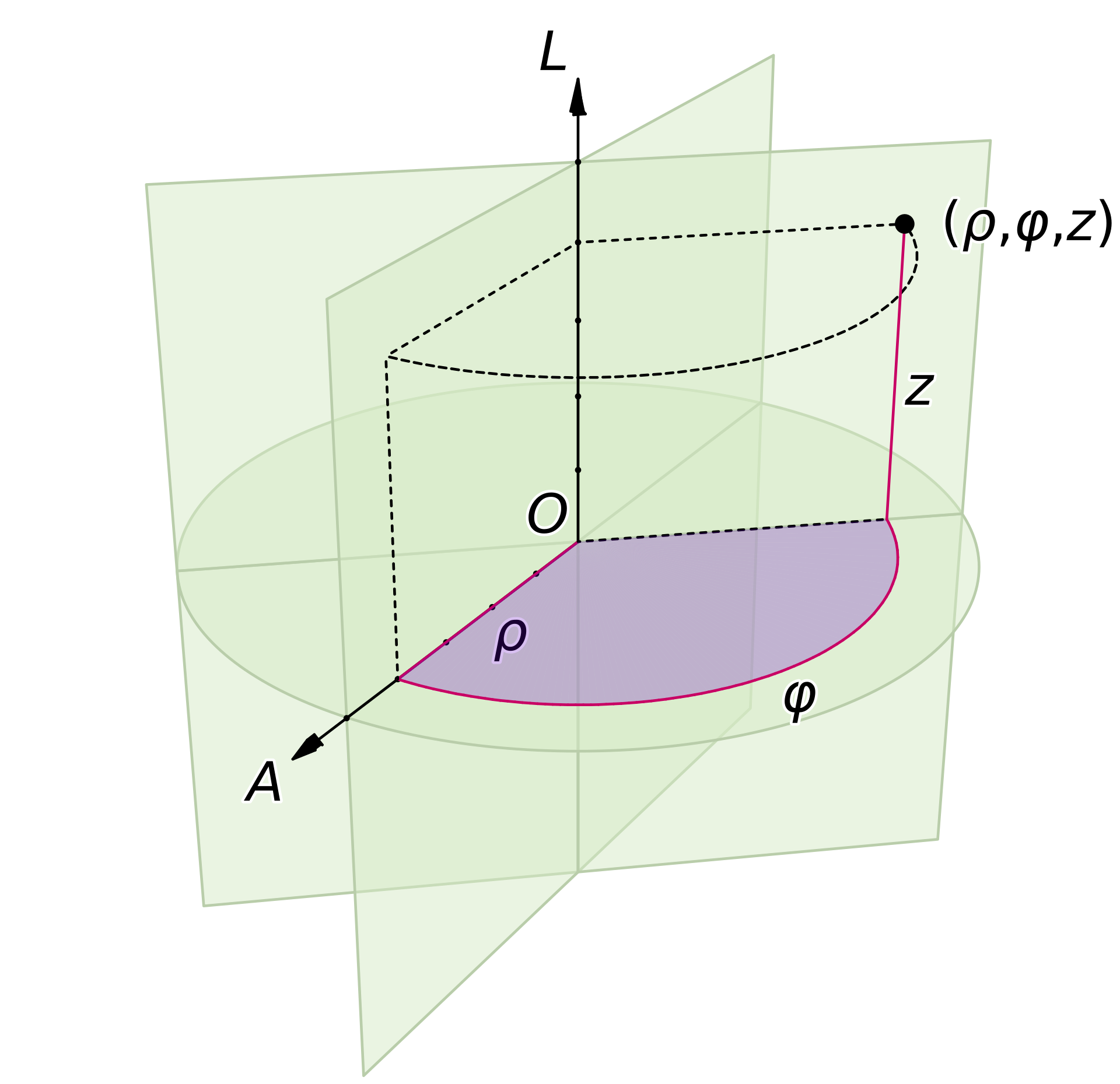
円筒座標系(Cylindrical Coordinates)は、三次元空間を角度・半径・高さで表す数学的座標系です。これを視覚化に応用したのが本チャートです。
特に 風向・風速・高度 、信号強度の方向特性 、極座標上の周期データの振幅変化 などを分析する際に有用です。
3D円筒散布図は、極座標プロット(Polar Plot)の三次元拡張とみなすことができます。二次元の極座標散布図では平面上の角度と距離で表現しますが、さらに高さ軸を加えることで、データの変化をより立体的に理解できます。
まとめ
三次元円筒座標散布図は、角度・距離・高さという3変数の関係を一度に把握できる強力な可視化手法です。
ドロップラインによって高さ情報が明確に示され、角度的な周期性と縦方向の変化を同時に読むことができます。
ただし、視点によっては奥行き方向の重なりが発生するため、適切な視角の設定やインタラクティブ表示が推奨されます。
参考・出典
- 3D surface with polar coordinates — Matplotlib ドキュメント:極座標/円筒座標を用いた 3D 表面描画例 oai_citation:0‡matplotlib.org
- Cylindrical Coordinates — Wolfram MathWorld:円筒座標系の定義および性質 oai_citation:1‡ウルフラム数学ワールド
- Cylindrical coordinate system — Wikipedia:座標系としての概要と応用例 oai_citation:3‡ウィキペディア
- Three-dimensional plotting in Matplotlib — Jake VanderPlas によるチュートリアル:「極座標グリッド」を 3D プロットに使う例 oai_citation:4‡jakevdp.github.io
