隣接行列(adjacency matrix)は、ネットワーク(グラフ)構造を行列の表形式で表現する方法です。つまり頂点(ノード)同士の接続関係を、行と列で示します。ネットワーク理論・社会ネットワーク分析・グラフアルゴリズムなどの分野で広く用いられています。
歴史的経緯
隣接行列は、グラフ理論の基礎的な表現方法として、コンピュータサイエンスや社会ネットワーク分析で早くから採用されてきました。特に、ノード数が少ない場合や、行列演算を通して連結性を計算する場合に適しています。
データ構造
(To be delivered.)
目的
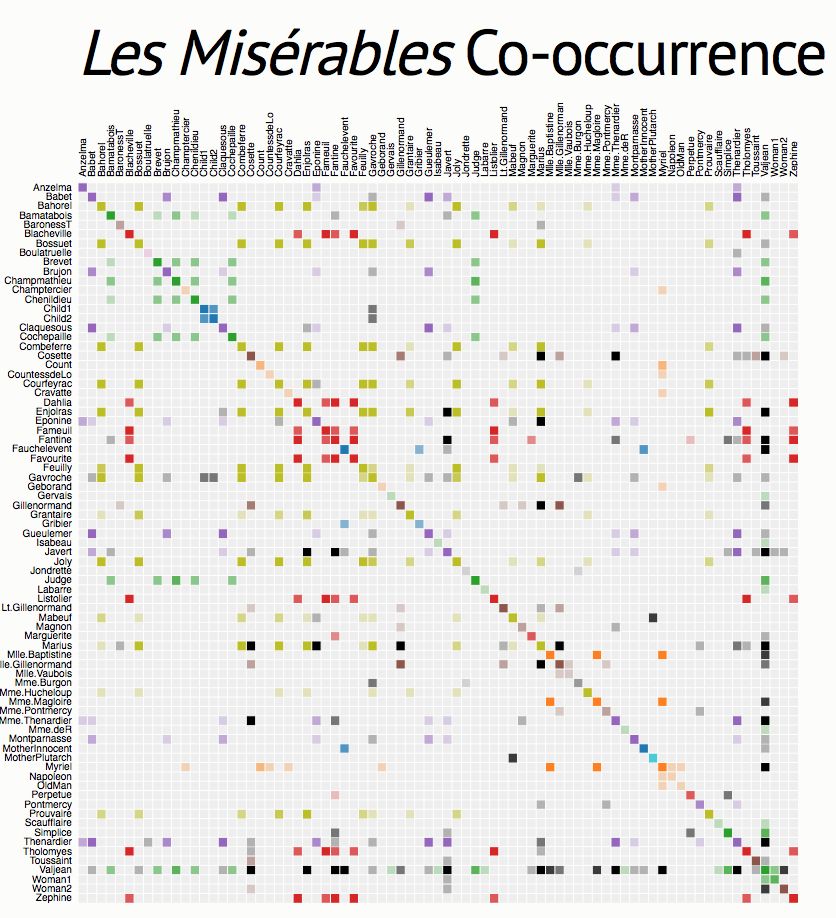
隣接行列は ネットワーク可視化の「行列型レイアウト」 として利用されます。
縦軸と横軸にすべてのノード(頂点)を並べ、交差点のセル(マス目)に「接続があるかどうか」を記します。
| 行・列 | 意味 | セルの値の意味 | 備考 |
|---|---|---|---|
| 行(縦) | 出発ノード(From) | 1(または◯):接続あり 0(または空白):接続なし | 有向グラフでは「出発点」を示す |
| 列(横) | 到達ノード(To) | 1(または◯):接続あり 0(または空白):接続なし | 無向グラフでは行列が対称になる |
| 対角成分 | 自己ループ | 1の場合:ノードが自分自身へ接続 | 多くのネットワークでは0 |
例えば、3つのノード A, B, C のネットワークで
A→B、B→C、C→A という接続がある場合の隣接行列は次の通りです。
| A | B | C | |
|---|---|---|---|
| A | 0 | 1 | 0 |
| B | 0 | 0 | 1 |
| C | 1 | 0 | 0 |
このように、行列の1つ1つのセルがエッジ(辺)を表すため、リンクの有無を簡潔に比較できます。
ユースケース
(To be delivered.)
特徴
ノードを円や線で描く「ノードリンク図」に比べ、リンクの重なりがなく 構造的な規則性(クラスター、対称性、自己ループなど) を視覚的に発見しやすい特徴があります。
| 可視化形式 | 特徴 | 適用例 |
|---|---|---|
| ノードリンク図 | 直感的・空間的関係を表現 | 小規模ネットワーク |
| 隣接行列 | 構造・関係パターンを強調 | 大規模・密集ネットワーク、社会ネットワーク |
長所
- 行列演算が使えるため、ネットワークの 連結成分・経路探索・中心性計算 に有効。
- 形式が単純で プログラム実装や保存 に適する。
短所
- ノード数が増えると、要素数が急増(O(n²))し、疎なネットワークでは 非効率 。
- 視覚的な理解が難しく、大規模ネットワークでは 密集したパターン(hairball) になりやすい。
チャートの見方
(To be delivered.)
デザイン上の注意点
(To be delivered.)
応用例
- ソート済み隣接行列(Sorted Adjacency Matrix):ノードを特定の属性(例:コミュニティ、次数、モジュール)で並べ替え、構造的パターンを強調。
代替例
- 相関行列との比較:隣接行列が「接続の有無(binary)」を表すのに対し、相関行列は「関係の強さ(continuous)」を示す。
- BioFabric・Hive Plotなど:隣接行列の欠点を克服し、構造を線形・規則的に描く手法として発展している。
まとめ
隣接行列は ネットワークを数値的・構造的に理解するための基本フォーマット であり、可視化においても「構造の秩序を読む」ことを重視する設計思想に通じています。ノード間の関係を抽象的に捉える練習として、インフォグラフィックス教育でも有効な素材となります。
