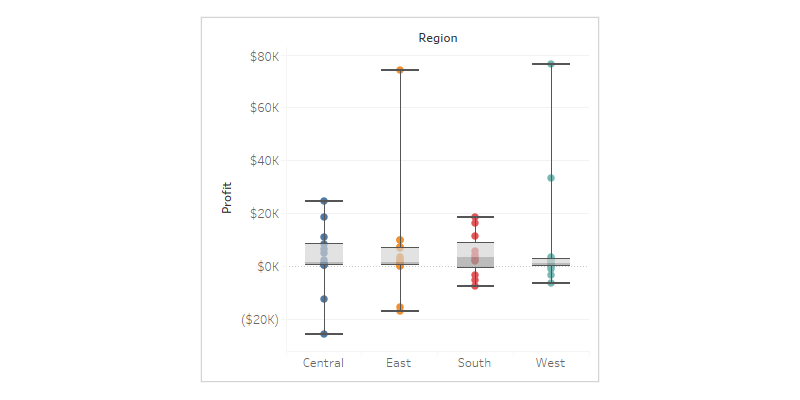
箱ひげ図(Box-and-Whisker Plot)は、データの分布を視覚的に要約し、外れ値や偏りを直感的に把握できる統計グラフです。データの最小値、第1四分位数(Q1)、中央値(Q2)、第3四分位数(Q3)、最大値を用いて構成され、箱(ボックス)は四分位範囲(IQR=Q3−Q1)を表します。箱から伸びる「ひげ(Whisker)」はデータの広がりを示し、外れ値は点で描かれることが一般的です。
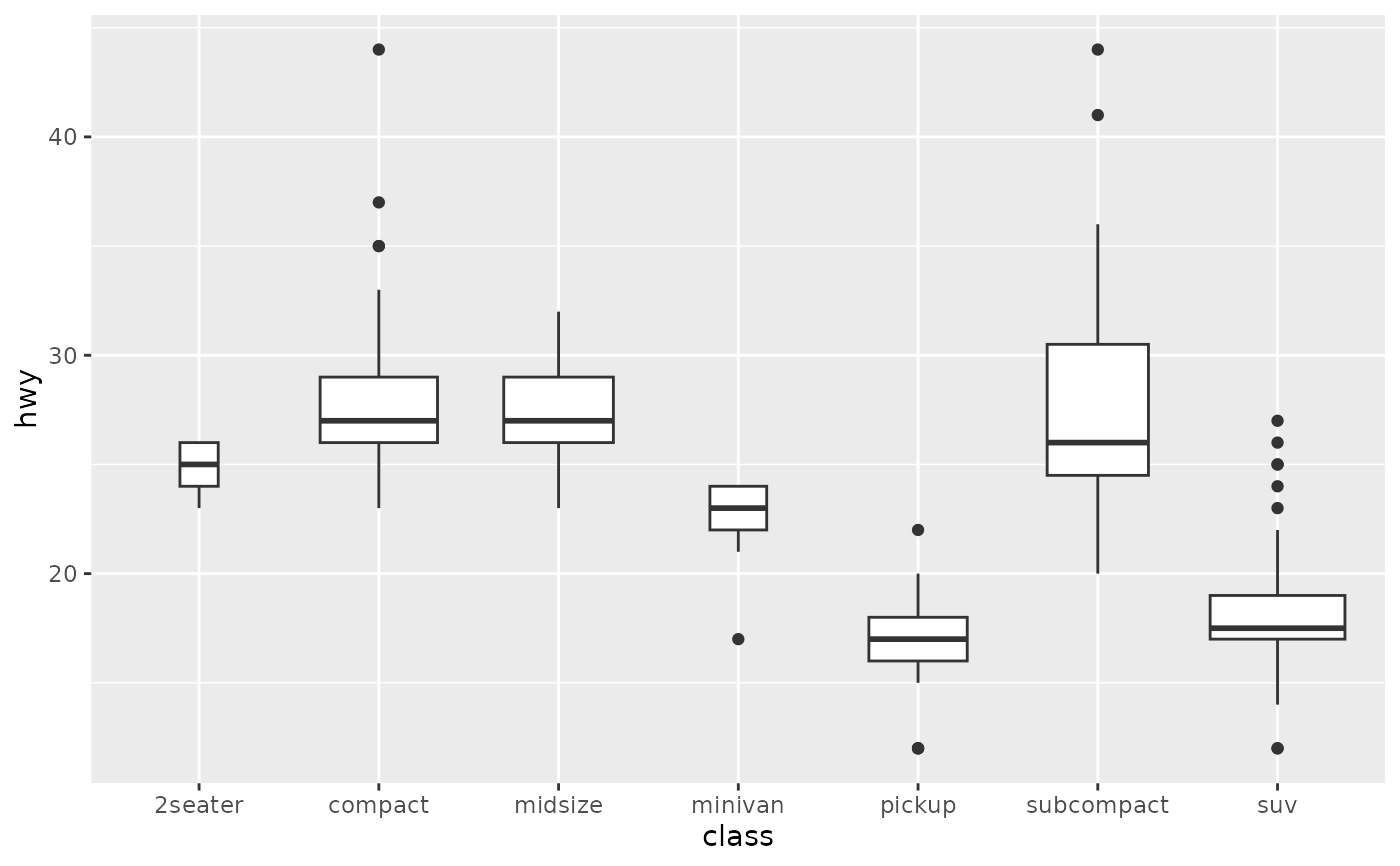
歴史的経緯
箱ひげ図は1970年代にアメリカの統計学者ジョン・W・テューキー(John W. Tukey)が提唱しました。彼の著書『Exploratory Data Analysis(1977)』において、データの特徴を探索的に理解する手法の一つとして紹介されました。それ以前は平均値や分散などの単一指標でデータを把握するのが主流でしたが、テューキーは視覚的・直感的な統計理解の重要性を強調しました。
データ構造
箱ひげ図に必要なデータ構造は、基本的に**単変量(1変数)**の数値データです。複数のカテゴリを比較する場合は、カテゴリごとに箱ひげを並べて描画します。主に以下の5つの統計量(「5数要約」)を用います。
| 指標 | 意味 |
|---|---|
| 最小値 | データの最小値(ただし外れ値を除く) |
| 第1四分位数(Q1) | データの下位25%点 |
| 中央値(Q2) | データの中央値 |
| 第3四分位数(Q3) | データの上位75%点 |
| 最大値 | データの最大値(外れ値を除く) |
目的
箱ひげ図の目的は、データのばらつきや偏り、外れ値の有無を視覚的に示すことです。平均値に依存しないため、外れ値に強いロバストな分布比較が可能です。また、グループ間の分布差を直感的に比較するのに適しています。
ユースケース
箱ひげ図は、複数のカテゴリやグループ間で分布を比較する際に非常に有効です。例えば、男女別の試験点数や年度別の売上分布などを同一スケールで比較できます。また、外れ値(異常値)の検出にも適しており、データ品質確認や異常検知の初期分析でもよく用いられます。
- 成績分布の可視化(クラスごとの得点分布)
- 品質管理(製造工程でのばらつき検出)
- 医療・生物統計(臨床データのばらつき)
- データ分析の初期段階での探索的可視化(EDA)
特徴
- 平均値ではなく中央値を基準とする
- 外れ値を明示的に可視化できる
- 分布の偏り(右裾/左裾)を容易に把握できる
- 複数グループの比較が容易
チャートの見方
| 要素 | 意味 | 表現 |
|---|---|---|
| 最小値 (Minimum) | データの最も小さい値 | 左端のひげの先端 |
| 第1四分位数 (Q1) | 下位25%の境界 | 箱の左端 |
| 中央値 (Median, Q2) | データの中心 | 箱内の線 |
| 第3四分位数 (Q3) | 上位25%の境界 | 箱の右端 |
| 最大値 (Maximum) | データの最も大きい値 | 右端のひげの先端 |
| 四分位範囲 (IQR = Q3 - Q1) | 中央50%のばらつき | 箱の幅 |
| 外れ値 (Outliers) | 1.5×IQRを超える値 | ひげの外に点で表示 |
箱の中の線が箱の中央より左にある場合は分布が右に歪んでおり、右にある場合は左に歪んでいると読み取れます。ひげの長さの非対称性は分布の偏りを、箱の大きさは中間データの散らばりを示します。
デザイン上の注意点
- 箱の幅は統一する(データ数に比例させると誤解を招くことがあります)
- スケールを固定して比較する(縦軸の範囲が異なると誤解されやすい)
- 外れ値の表現は一貫させる(点・星印など)
- 色を使う場合はカテゴリ区分を明確にする
- 背景グリッドや補助線を適度に配置して読みやすくする
応用例
近年では 変形版として「バイオリンプロット(Violin Plot)」や「ビーズプロット(Beeswarm Plot)」 など、分布形状の情報をより詳細に付加したバリエーションも登場しています。ただし、箱ひげ図はあくまで5点要約(five-number summary)に基づく可視化であり、分布の形状(例えば双峰性や歪度)を完全に表現するものではありません。
- バイオリンプロット(Violin Plot):箱ひげ図に分布密度を加えた形式。密度の形状を視覚化できる。
- ビースウォームプロット(Beeswarm Plot):個々のデータ点を重ならないように配置して分布を直に示す。
- スウォーム+箱ひげのハイブリッド型:SeabornやPlotlyでは箱ひげと点分布を重ねて表現することが可能。
代替例
| チャート名 | 特徴 | 適用シーン |
|---|---|---|
| ヒストグラム | 階級ごとの頻度を表示 | 分布の形を把握したい場合 |
| バイオリンプロット | 密度形状を含めて分布を表示 | 分布の滑らかさや多峰性を見たい場合 |
| ストリッププロット | 個々の値を可視化 | サンプルサイズが小さい場合 |
まとめ
箱ひげ図は、分布の特徴を簡潔に要約し、比較や外れ値検出を支援する基本的な統計グラフです。データの散らばりや偏りを直感的に理解できるため、探索的データ分析やレポート作成、教育など幅広い分野で利用されています。
EDA(探索的データ分析)における基本的かつ不可欠な可視化手法として、今なお多くの分野で利用されています。
ただし、平均値や標準偏差の情報は含まれないため、必要に応じて他の可視化(ヒストグラム・密度プロットなど)と併用するのが望ましいです。
参考・出典
- Box plot — Wikipedia
- Understanding Boxplots — Towards Data Science
- Seaborn Boxplot Documentation
- Plotly Box Plot Documentation
- Box plot - Wikipedia
- Build a Box Plot — Tableau Help
- Box and Whisker Plots — The Data Visualisation Catalogue
- 1.3.3.7. Box Plot — NIST/ITL Engineering Statistics Handbook
- Box plot review — Khan Academy
- geom_boxplot — ggplot2 reference