1973年、統計学者ハーマン・チャーノフはちょっと風変わりなアイデアを論文で発表しました。タイトルは「The Use of Faces to Represent Points in K-Dimensional Space Graphically」。 直訳すれば「K次元空間の点を顔で表現する方法」です。
多次元データをどう見せるか
データ分析をしていると、変数が5個、10個と増えていくことはよくあります。けれど、縦横2軸しかないグラフでは表しきれない。数字の表を眺めていても頭に入ってこない。 そんなとき、チャーノフは「顔にしてしまえばいいのでは?」と考えました。
仕組みはシンプル
- データの各変数を、顔のパーツに割り当てます。
- 1つのデータ=1枚の「顔」として描かれます。
- 似たデータは似た顔に、極端に違うデータは異様な顔に。
つまり、数字の塊が「表情」として私たちの目に飛び込んでくるのです。
なぜ「顔」なのか
人間は顔の違いにとても敏感です。ほんの少し口角が下がっているだけで「怒っている?」と感じたり、眉が上がっているだけで「驚いている?」と思ったりします。 チャーノフはこの能力をデータ分析に応用しました。数字を数字のまま読むより、顔の違いとして認識したほうが直感的に理解できる、という狙いです。
さらに興味深いのは、その発想の逆転です。当時の人工知能研究は「人間の顔を数値に変換し、機械に識別させる」ことに力を注いでいました。ところがチャーノフはその逆で、「数値を顔に変換し、機械には顔を描かせ、人間に識別させる」方法を選びました。彼の言葉を借りれば 「顔を描くという重労働は機械に任せ、知能は人間に委ねる」 という発想です。
論文の図版と解説
実際の論文には、チャーノフが生成した「顔の配列」が数多く掲載されています。どの変数をどのパーツに割り当てるかで、同じデータでもまったく違った印象の顔が並びます。
顔の表情からクラスターを見つける

| 顔の部分 | 変数 | データの意味 |
|---|---|---|
| 顔の角への半径 (x₁) | Z₁ | 胚室の内径(ミクロン) |
| 顔の垂直サイズ (x₃) | Z₃ | 第1巻の室数 |
| 下顔の離心率 (x₅) | Z₄ | 最終巻の室数 |
| 鼻の長さ (x₆) | Z₅ | 第1巻の室の最大高さ(ミクロン) |
| 口の垂直位置 (x₇) | - | 固定値 |
| 口の曲率 (x₈) | - | 固定値 |
| 口の幅 (x₉) | - | 固定値 |
| 目の垂直位置 (x₁₀) | - | 固定値 |
| 目の間隔 (x₁₁) | - | 固定値 |
| 目の傾斜 (x₁₂) | Z₆ | 最終巻の室の最大高さ(ミクロン) |
| その他の特徴 | - | 固定値 |
統計学でいう「多変量データ」(一つの対象に複数の測定値があるデータ)は、数値の羅列になりがちです。この数値の海の中から、互いに似ているデータ群、つまり クラスター(集団) を見つけ出すのは至難の業です。もしその複雑なデータを、私たちの脳が最も得意とする「 顔 」の形として表現できたらどうでしょうか?
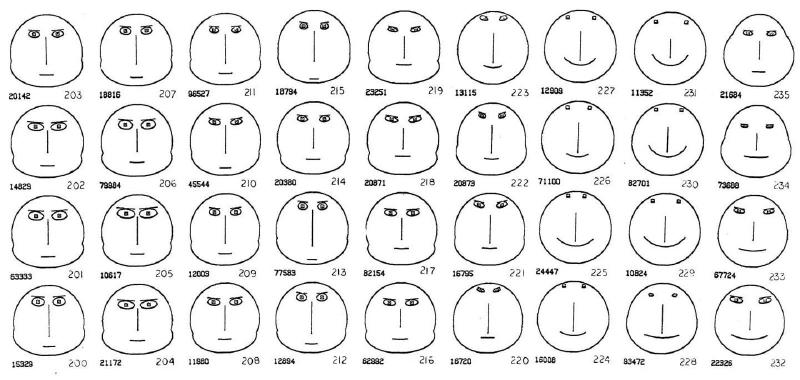
図1Aで示されているのは、ジャマイカ北西部から採取された 87個の有孔虫(Nummulited)化石標本 のデータ(6つの異なる測定値)を顔に変換したものです。各化石が持つ6つの特性が、その顔のパーツの形や大きさに変換されています。
化石データに関心を持っていた調査者のタスクは 「互いに似ている顔を単にグループ化する」 ことでした。図1Aに表示された87個の顔は、事前に解析技術によって 3つの明確なクラスター にグループ分けされた後、その分類が際立つように順序立てて提示されました。その結果、これらの顔の集まりが 「一目瞭然に」3つの異なるクラスターに分かれている ことが確認されました。
さらに興味深いのは、この顔の図を、データに関する事前情報やID番号を隠した状態で一般の人々に見せて、視覚的に分類してもらったところ ほとんどの人が統計解析と同じクラスターを選択した という事実です。
これは、この「顔」の表現方法が、人間の心が持つ 複雑な視覚現象の中から、重要ではないものをフィルタリングし、潜在的に重要な情報に焦点を当てる という高い能力(高速度コンピューターのような働き)を活用していることを示しています。顔による表現は、クラスター分析の支援に非常に有効であるとしています。
顔の表情から時系列の変化を見つける
| 顔の部分 | 変数 | データの意味 |
|---|---|---|
| 顔の角への半径 (x₁) | Z₁ | 鉱物含有量データ |
| 顔の垂直サイズ (x₃) | Z₃ | 鉱物含有量データ |
| 上顔の離心率 (x₄) | Z₂ | 鉱物含有量データ |
| 下顔の離心率 (x₅) | Z₄ | 鉱物含有量データ |
| 鼻の長さ (x₆) | Z₅ | 鉱物含有量データ |
| 口の垂直位置 (x₇) | Z₆ | 鉱物含有量データ |
| 口の幅 (x₉) | Z₅ | 鉱物含有量データ |
| 目の垂直位置 (x₁₀) | Z₉ | 鉱物含有量データ |
| 目の間隔 (x₁₁) | Z₁₀ | 鉱物含有量データ |
| 目の傾斜 (x₁₂) | Z₁₁ | 鉱物含有量データ |
| 目の離心率 (x₁₃) | Z₁₂ | 鉱物含有量データ |
| 眉毛の垂直位置 (x₁₆) | Z₇ | 鉱物含有量データ |
データが時間の経過や物理的な距離に沿って連続している 時系列データ を扱う場合、私たちは「いつ、どこで、そのデータの特性が大きく変化したか」を知りたいと考えます。しかし、12もの変数が絡み合うような多次元の時系列データを数値で追いかけると、重要な変化の瞬間を見逃しがちです。ここで、「顔の表現」が強力なツールとなります。
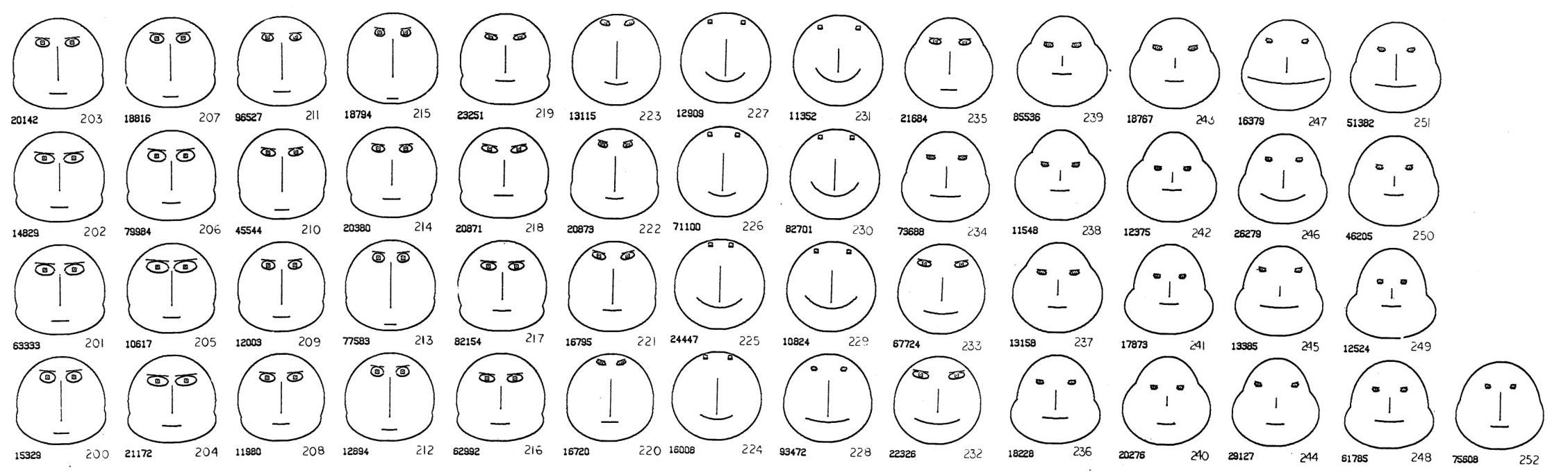
図2に示されているのは「地質データ」の事例です。これは、コロラドの山腹から掘削された4,500フィートのコアから採取された 53個の等間隔の標本 に基づいています。各標本は、7つの鉱物含有量やその再分析結果を含む 12個の変数 を持っています。
53個の顔は、コアの順序(時系列順)で表示されています。調査者のタスクは 「多変量確率過程が特性を変化させた時間点」 つまり顔の特性が変化した場所を特定することでした。
顔を順に見ていくと、標本 219 の後に一つの大きな変化が始まり、特に 224から231 に対応する顔のグループが、他の顔とは 「全く異なっている」 ことがわかります。
次に、標本 231から234 にかけて、別の大きな変化が進行していることも読み取れます。
そして 235から252 のグループは、また 別の異なる特徴が示されています。
この12次元の時系列データに対して、もし従来の線形分析が適用されていたとしたら、顔を見ることで明確に観察できるこの種の現象が 「覆い隠されてしまう可能性」 があることが示唆されています。人間が顔から直感的に得られる情報は、標準的なコンピュータープログラムに欠けている「柔軟性」を補い、重要な現象の検出を可能にする、としています。
面白さと落とし穴
この方法にはユニークさと同時に、いくつかの弱点もあります。
- 主観的:どの変数をどのパーツに割り当てるかで顔の印象は大きく変わる。
- 正確さに欠ける:目の大きさや口の曲線を定量的に比較するのは難しい。棒グラフほどの厳密さはない。
- 感情を帯びやすい:口が下がっている顔は「悲しい」と感じるなど、データに関係ない印象が入り込む。
まとめ
チャーノフの顔は、
- 「数字を顔にする」という大胆な発想
- 人間の認知特性をうまく利用した工夫
- 今なお語られるユニークなビジュアライゼーション
ということを提示しました。