ハイパーボリック・ツリー(Hyperbolic Tree)は、階層構造データ(ツリー構造)を円形のハイパーボリック空間上に可視化する手法です。通常のツリーダイアグラムでは、階層が深くなるにつれて描画領域が不足しやすくなりますが、ハイパーボリック幾何学を応用することで、中心に近い要素を拡大し、周辺に向かうほど圧縮する形で広範な階層を一度に表示できます。このため、情報の全体像を把握しつつ、部分的な詳細にも焦点を当てる「フォーカス+コンテキスト(Focus + Context)」可視化の代表的な例とされています。
歴史的経緯
ハイパーボリック・ツリーは、1990年代半ばに研究者Tamara Munznerらによってスタンフォード大学およびXerox PARCで開発されました。特に1995年の論文「Hyperbolic Tree: A Visualization for Browsing Large Hierarchies」において、その理論的背景と実装手法が提示されました。当時は大規模な情報構造(例えばファイルシステムやウェブサイト階層)のナビゲーションを課題としており、従来のツリー図に代わる新しいインタフェースとして注目を集めました。その後、Javaアプレット版「Hyperbolic Browser」としてウェブ上でも広く公開され、視覚化研究やユーザインタフェース設計に大きな影響を与えました。
データ構造
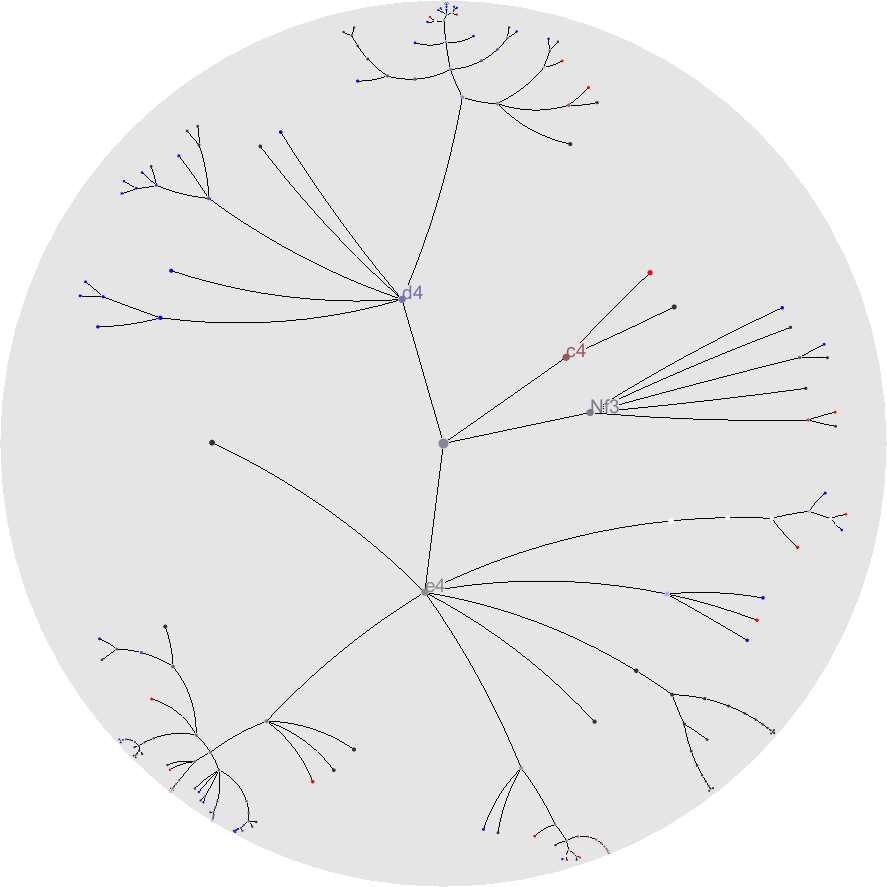
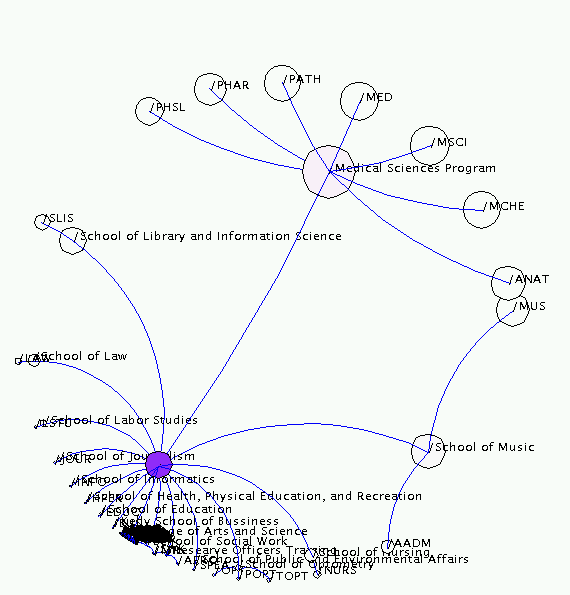
扱うデータは典型的なツリー構造(ノードとエッジの階層的関係)です。各ノードが親子関係を持ち、ルートから枝分かれしていく構成です。ハイパーボリック空間上では、ユークリッド平面の代わりに「双曲面(Poincaré disk model)」を用い、ノードを円盤内に配置します。この幾何学的圧縮により、中心部分のノードは大きく、外周部は小さく描かれますが、全体の関係性は保持されます。
目的
主な目的は、大規模な階層構造をスクロールやズームを行わずに一度に視覚的に理解できるようにすることです。ユーザーは特定のノードを中心に移動することで関心領域を拡大しつつ、周囲の文脈を失わずに探索できます。
ユースケース
- 企業組織図や製品分類ツリーの可視化
- ファイルシステムやウェブサイト階層のナビゲーション
- 辞書・語彙関係などの意味ネットワークの探索
- ソフトウェア構造(クラス・モジュール階層)の可視化
- Webサイトやフォルダ階層の可視化
- 系統樹や生物分類の表示(Tree of Lifeプロジェクトなど)
- 大規模ネットワークや知識グラフのブラウジング
- ハイパーボリック埋め込みを利用したグラフ学習モデル(Hyperbolic Graph Embedding)
特徴
| 特徴 | 説明 |
|---|---|
| 幾何モデル | ハイパーボリック(双曲)空間を利用 |
| 表示領域 | 中心部は拡大、外周は圧縮 |
| 操作性 | ドラッグによる中心移動で動的に焦点を切り替え |
| 利点 | 広い階層を一画面で表示可能 |
| 欠点 | 幾何的歪みにより直感的距離感が失われやすい |
通常のツリーレイアウトでは、ノード数が増えるほど枝が指数的に増加し、全体を一画面で表現するのが難しくなります。これに対してハイパーボリック・ツリーは、負の曲率を持つ「双曲空間」にツリーを埋め込み、中心から外側に向かってノードを配置します。この空間では、同じ半径でも円周の長さが指数的に広がるため、多数のノードを円盤内に収められるという利点があります。
可視化の際は、双曲平面を ポアンカレ円板モデル(Poincaré disk model) に写像して表現します。中心には注目ノード(focus)があり、周囲にコンテクスト(context)として関連ノードが縮小されながら配置されます。ユーザーは任意のノードをクリックして再中心化(re-centering)することで、ツリーを動的に探索できます。
チャートの見方
中央に最も注目しているノード(ルートまたは選択ノード)が配置され、その周囲に子ノードが放射状に展開されます。ユーザーがノードをクリックまたはドラッグすると、そのノードが新たな中心に移動し、全体が再配置されます。視覚的には「ズーム」しているように見えますが、実際にはハイパーボリック変換による幾何学的な再描画です。
ハイパーボリック・ツリーの典型的な表示では、以下のような構造になっています。
- 中央(Focus Node):現在の注目ノード。
- 周辺ノード(Context Nodes):関連する親・子ノード。距離が遠いほど小さく表示される。
- リンク(Edges):ノード間の階層関係を示す線。双曲空間上では曲線として描かれる。
- 再中心化操作:任意のノードをクリックすると、そのノードが新たな中心となり、周囲が再配置される。
この「フォーカス+コンテクスト(focus+context)」のアプローチにより、ユーザーは全体構造を見失うことなく、部分構造をズーム的に探索できます。
デザイン上の注意点
- ノード間の重なりを避け、階層が深いほど小さく表示するバランス調整が重要です。
- 色や線の太さによって、階層レベルや重要度を示すと理解しやすくなります。
- 中心移動時のアニメーションを滑らかにすることで、ユーザーの認知負荷を下げます。
応用例
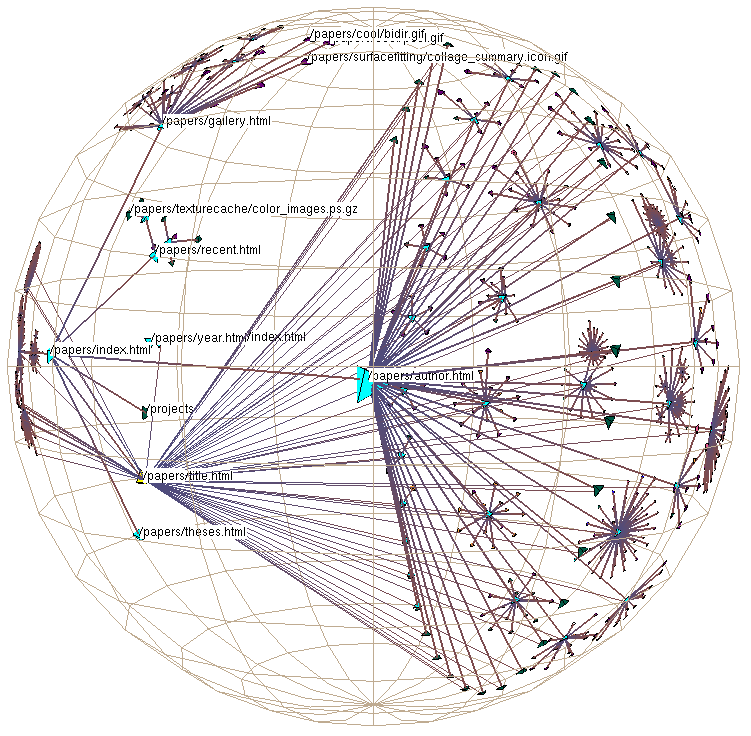
- Walrus Visualization Tool(CAIDA, 2000年代初頭):インターネットトポロジーの可視化にハイパーボリック・ツリーを採用。
- WebTree:ウェブサイト階層を探索するためのブラウザ型インタフェース。
- 情報アーキテクチャ設計:情報構造の俯瞰ツールとして研究・教育に利用。
代替例
- サークルパッキング(Circle Packing):階層を円で表す手法。
- サンバースト(Sunburst)やアイシクル(Icicle)チャート:階層を角度や長さで表現する手法。
- ツリーマップ(Treemap):面積分割による階層可視化。
これらはいずれもツリー構造を異なる形で表現する手法であり、ハイパーボリック・ツリーは「対話的階層ブラウジング」に特化しています。
まとめ
ハイパーボリック・ツリーは、限られた画面空間で広大な階層データを探索するために開発された革新的な可視化手法です。数学的に洗練された双曲空間の原理を応用し、フォーカス+コンテキスト型インタフェースの代表例として現在も情報視覚化の研究・実装に多くの影響を与えています。
参考・出典
- CAIDA Walrus Visualization Tool
- Xerox PARC Hyperbolic Browser Project
- Hyperbolic tree — Wikipedia
- Hyperbolic Trees — InfoVis CyberInfrastructure (Indiana University)
- Hyperbolic Tree — DataVizProject
- H3: Laying Out Large Directed Graphs in 3D Hyperbolic Space — Tamara Munzner (Stanford University)
- Hypertree.js — Nicolas Garcia Belmonte
- The Green Tree of Life — Hyperbolic Tree Viewer (UC Berkeley)
