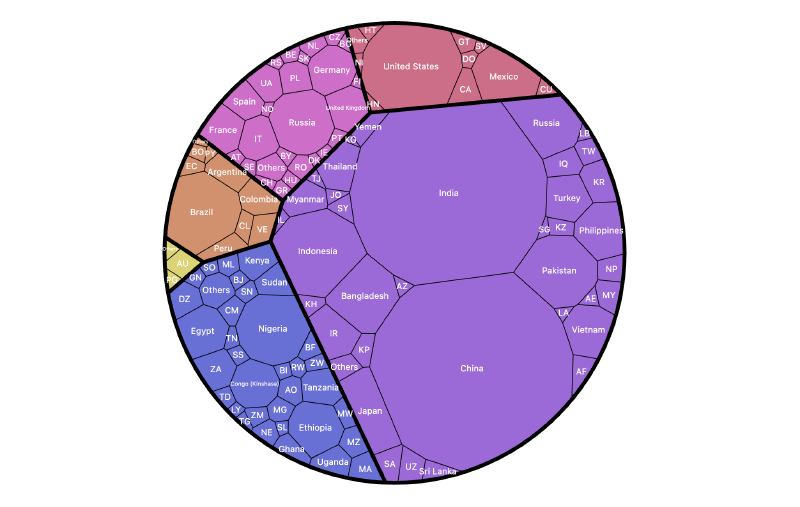
円形ボロノイ・ツリーマップ（Circle Voronoi Treemaps）は、ボロノイ図（Voronoi Diagram）を応用して階層構造データを不規則な多角形で空間分割する領域分割型の可視化手法です。通常のツリーマップが長方形で空間を分割するのに対し、円形ボロノイ・ツリーマップは円形の外枠内でボロノイ分割を行い、より自然で有機的なレイアウトを実現します。要素同士の関係や重心配置を視覚的にわかりやすく表現できる点が特徴です。
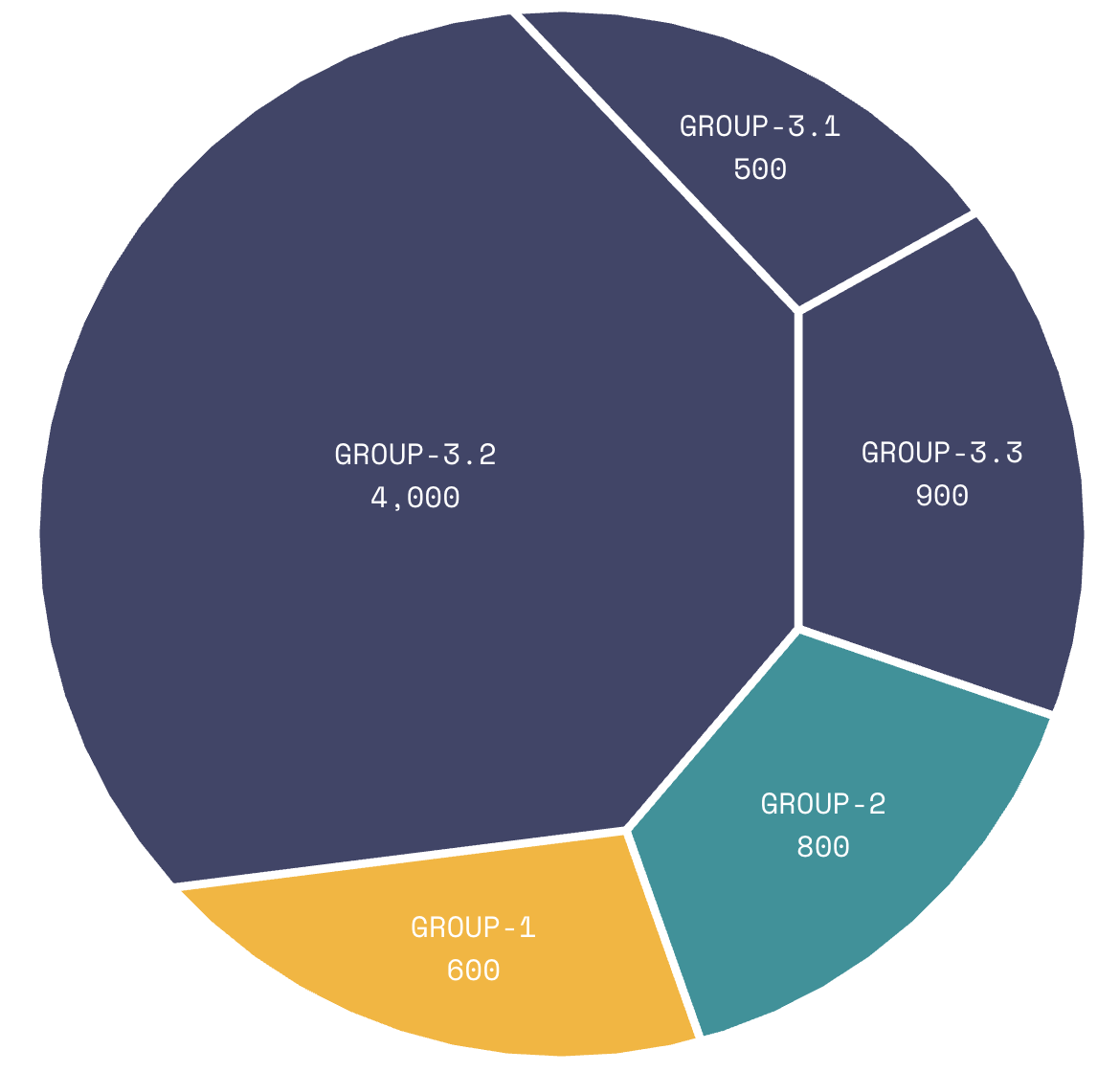
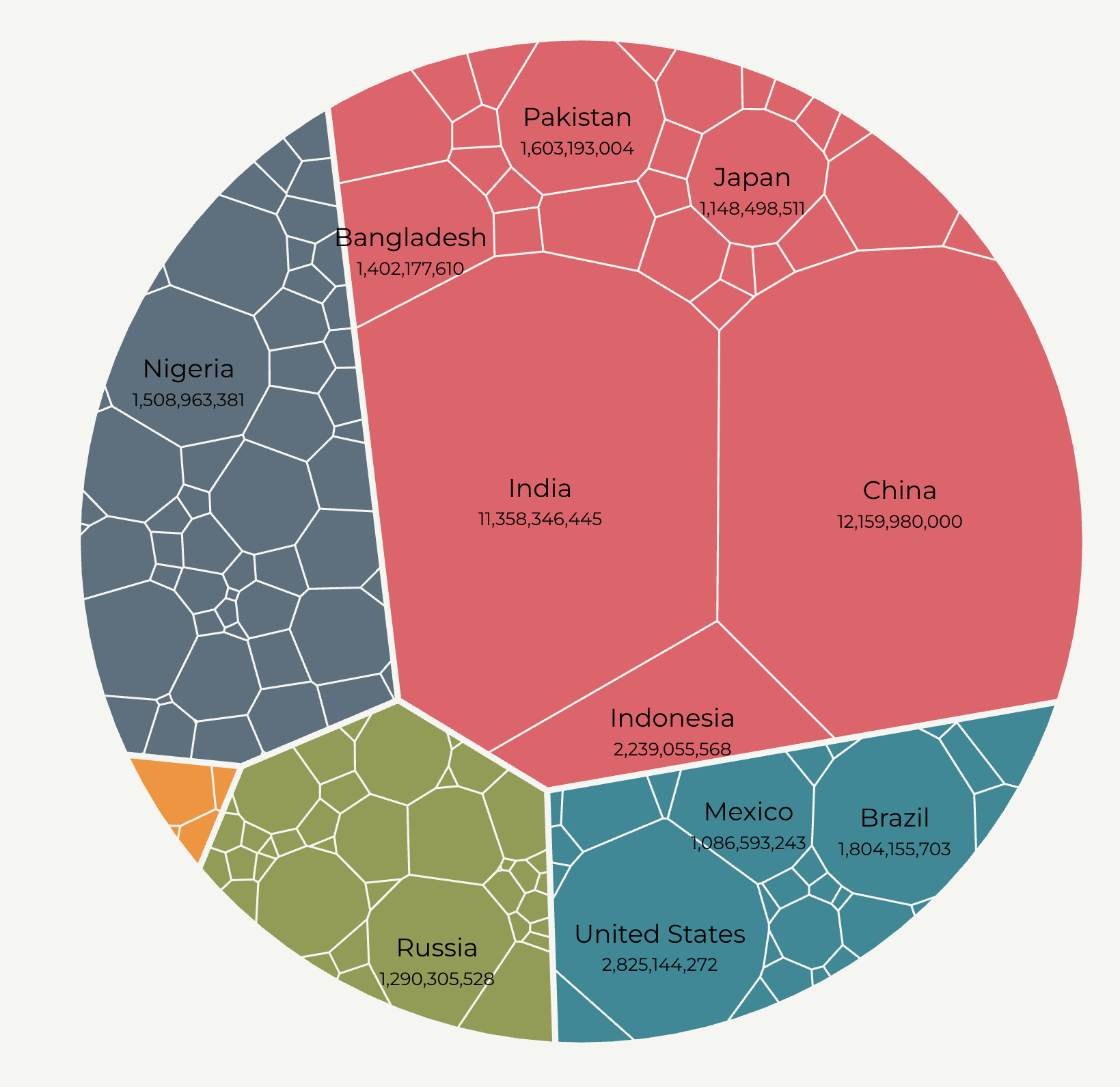
歴史的経緯
ボロノイ・ツリーマップは、2000年代初頭にドイツの研究者によって提案された比較的新しい手法です。特にMichael BalzerとOliver Deussen（2005年）による論文「Voronoi Treemaps for the Visualization of Hierarchical Data」が基礎となっています。この研究は、従来の長方形ツリーマップの欠点（縦横比の極端な矩形、視認性の低下など）を克服する目的で行われました。その後、D3.jsやProcessingなどの可視化ライブラリでもボロノイ分割を用いた階層可視化が実装され、改良が重ねられています。円形の外枠を用いるバリエーションは、全体の形状がコンパクトにまとまり、視覚的なバランスが良い表現として注目されています。
データ構造
| 項目 | 内容 | 例 |
|---|---|---|
| ノード（Node） | 階層内の各要素 | 部門名、生物分類名、ファイル名 |
| 親子関係（Parent-Child） | ノード間の包含関係 | ドメイン-サブカテゴリ-アイテム |
| 値（Size/Value） | 面積にマッピングする数値 | 売上、人口、ファイルサイズ |
| カテゴリ（任意） | 色で区別する分類 | 業種、地域、種類 |
| 重心座標（計算用） | レイアウトアルゴリズムが内部的に使用 | ボロノイ分割の母点座標 |
目的
円形ボロノイ・ツリーマップの主な目的は、階層データをより自然な形状で空間的に表現し、構造全体のバランスや要素間の関係性を直感的に理解しやすくすることです。矩形ベースのツリーマップと比べて、空間の使い方が有機的であり、美的な訴求力も高い表現が実現できます。
ユースケース
- 企業の組織構造や部門別の構成比を有機的な形状で可視化する
- 生態系や生物分類など、階層的分類データを自然な形状で表示する
- ファイルシステムの構造や使用容量を円形の中で視覚化する
- 都市・地域構造データの階層的可視化（例：地域、区、町、建物）
- ニュースやトピックの分類と分量を直感的に把握するメディアダッシュボード
特徴
| 特徴 | 説明 |
|---|---|
| 不規則な形状 | 自然界や地理的構造を連想させる有機的な形状で表現できます |
| 領域の連続性 | 境界がなめらかに接続し、区画間のつながりが視覚的に保たれます |
| 比例面積 | ノードの値に応じて面積を比例的に割り当てることが可能です |
| 高い美的価値 | 長方形に比べ、有機的で柔らかな印象を与えます |
| 円形外枠 | 全体がコンパクトにまとまり、視覚的バランスが良くなります |
チャートの見方
| 要素 | 説明 |
|---|---|
| セル（領域） | 各データ項目を示し、ボロノイ分割によって生成された多角形として表示されます |
| サイズ | 各領域の面積はデータの値（売上、人数、割合など）に比例して割り当てられます |
| 色 | 階層構造のレベルやカテゴリを区別するために用いられます |
| 境界線 | 隣接する領域との境界を示し、階層レベルに応じて線の太さやスタイルが異なることがあります |
| 位置 | 関連するカテゴリーは物理的にも近い位置に配置され、分布全体の「まとまり感」を強調します |
デザイン上の注意点
- 形状が不規則になるため、ラベル配置が難しい点に注意が必要です。セルの面積が十分に大きい場合のみラベルを表示する工夫が有効です
- 色分けや階層境界を明示する工夫（境界線の太さや色の変化）が求められます
- 階層レベルが深い場合、インタラクティブなズーム機能を組み合わせると効果的です
- 比例面積の誤差を最小化するため、重心ボロノイ分割（Centroidal Voronoi Tessellation）の反復計算を行うレイアウトアルゴリズムを採用します
- 小さなセルが密集すると視認性が低下するため、最小表示サイズの閾値を設定することを検討します
応用例
- 地図との融合：地理的エリアにボロノイ分割を重ねる「ジオ・ボロノイツリーマップ」として、地域データを有機的に表現する
- デザイン可視化：製品構成やアートワークの構造分析に用い、美的な表現として活用する
- 情報建築：Webサイト構造やナレッジマップの階層表示に使用し、サイトの構成を直感的に伝える
- 生物学的データ：種の分類と個体数を階層的かつ自然な形状で表現する
代替例
- 長方形ツリーマップ（Rectangular Treemap）：矩形で空間を分割する最も一般的なツリーマップ
- 円形パッキング（Circle Packing）：円の入れ子で階層を表す手法
- サンバーストチャート（Sunburst Chart）：放射状に階層を展開するチャート
- アイシクルチャート（Icicle Chart）：帯状に階層を並べる表現
まとめ
円形ボロノイ・ツリーマップは、階層データをより自然で直感的に可視化する手法として注目されています。矩形ベースのツリーマップに比べて美的表現力が高く、情報デザインや生物学的データ、地理情報などにも応用可能です。ボロノイ分割の幾何学的性質を利用することで、階層構造を「自然の中の分布」に近い形で理解できる点が大きな利点です。ラベル配置やレイアウト計算のコストに留意しつつ、適切な場面で活用することが効果的です。
参考・出典
| |