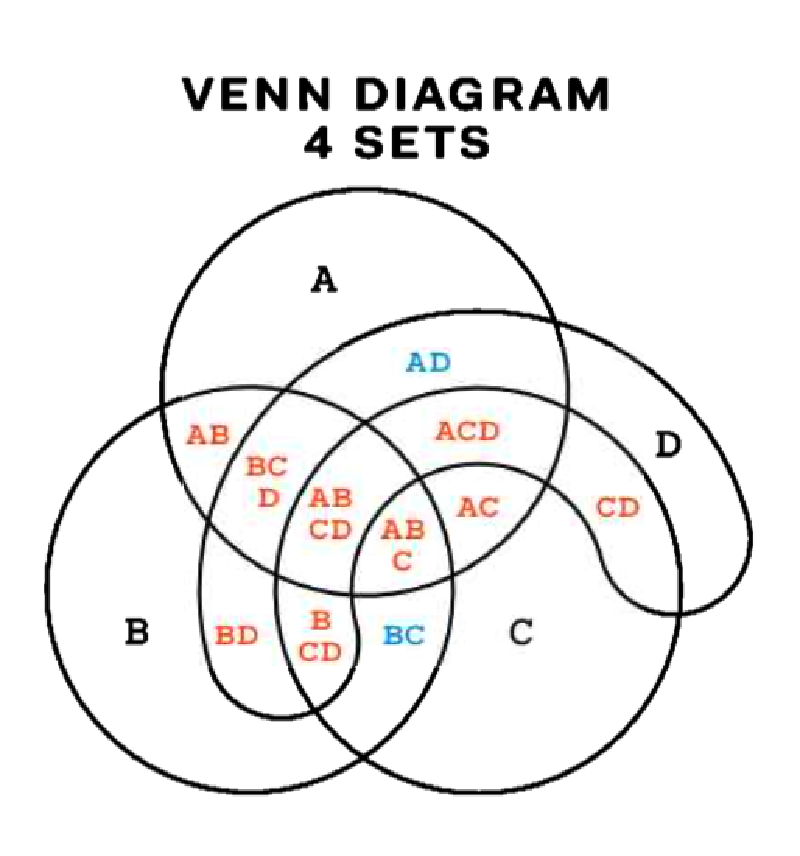
ベン図(Venn Diagram)は、集合の関係を図示するための可視化手法です。複数の集合を円や楕円で表し、それらの重なりによって共通部分(共通要素)や排他的部分を示します。主に論理学、確率論、集合論、データ分析などで、概念の包含・排除関係を直感的に理解するために用いられます。
歴史的経緯
ベン図は、イギリスの論理学者 ジョン・ベン (John Venn, 1834–1923) によって1880年に体系化されました。
彼の論文「On the Diagrammatic and Mechanical Representation of Propositions and Reasonings」において、複数の集合の包含関係を図示する方法として提案されたのが起源です。
ただし、集合関係を図で表す試み自体は18世紀の数学者 レオンハルト・オイラー (Leonhard Euler) にさかのぼります。オイラー図では、実際に存在する関係のみを描きますが、ベン図はすべての論理的な可能性(2ⁿ通り)を含む点が異なります。
つまり、ベン図はオイラー図を拡張し、論理的完全性を備えた体系として確立されたものです。
データ構造
ベン図の基本構成は以下の通りです。
| 要素 | 内容 |
|---|---|
| 集合 | 円や楕円で表現される対象群 |
| 要素 | 各集合に含まれる個々のデータや概念 |
| 共通部分 | 複数の集合が重なる領域で、共通の要素を示す |
| 排他的部分 | 他の集合と共有しない領域で、固有の要素を示す |
2集合ではA∩B、3集合ではA∩B∩Cといった論理積(AND)関係が明確に視覚化されます。
目的
ベン図は、2つまたは3つの集合関係を示す場合が多く、それぞれの領域が「共通部分」「差集合」「補集合」などの意味を持ちます。
ベン図の主な目的は、複数の集合の間に存在する共通点・相違点を視覚的に理解することです。特に、分類、条件分岐、論理的な重なりや排他関係を整理する際に有効です。教育現場でも、論理的思考を育てる教材として頻繁に用いられています。
数学・統計・情報科学・ビジネス分析など、幅広い分野で利用されています。
ユースケース
- 論理学・集合論:命題の関係を視覚的に示す。
- 確率論:事象AとBの同時確率、排他的確率などを説明。
- マーケティング:複数の顧客層やブランド認知の重なりを分析。
- データ分析:異なるカテゴリに属するデータ群の関係把握。
- 教育:共通点と相違点を整理する思考ツールとして使用。
特徴
- 概念的関係を 直感的に理解 できる。
- 少数の集合(2〜3程度) を扱うのに適している。
- 4集合以上になると視覚的に複雑になり、判読が困難になる。
- 数値よりも構造的関係の理解を重視する。
チャートの見方
- 各円は異なる集合を表す。
- 円が重なっている部分は、両方(または複数)の集合に共通する要素を示す。
- 円が重ならない部分は、それぞれの集合に固有の要素を表す。
- 3集合のベン図では、中央の小さな領域が「すべての集合に共通する要素」を意味します。
ベン図の基本構成は以下の通りです。
| 記号 | 意味 | 図中の位置関係 |
|---|---|---|
| (A) , (B) | 各集合 | 円や楕円で表される領域 |
| (A \cup B) | 和集合(どちらかに属する) | 2つの円のすべての部分 |
| (A \cap B) | 共通部分(両方に属する) | 2つの円の重なり部分 |
| (A - B) | 差集合(Aのみに属する) | AのうちBと重ならない部分 |
| (A^c) | 補集合 | 全体集合からAを除いた部分 |
デザイン上の注意点
- 重なりの色や透明度を調整し、交差領域を明瞭にする。
- ラベルの配置は重なりを避け、明示的に矢印などで指示する。
- 数量データを正確に表す目的(例:面積=要素数)には不向きであるため、数量比較には適さない。
- 多集合の場合は、オイラー図やUpSet Plotなどの代替手法を検討するとよい。
応用例
1. 教育・論理学
論理式の真理値表を視覚的に示したり、集合演算(和・積・補)の導入教材として利用されます。
2. データ分析
異なるデータ群(例:顧客層・購買層・Web閲覧層など)の重なりを示す際に用いられます。特にマーケティングやユーザー分析の分野では、要素の共通性を説明するための視覚ツールとして有効です。
3. コンピュータ科学
論理回路の設計、確率論、データベースの集合演算など、数理的な構造を理解する上でも用いられます。
4. ビジュアルデザイン・情報可視化
要素の関係を簡潔に伝える図として、スライド資料やインフォグラフィックスでも広く活用されています。
代替例
| 手法 | 概要 | 適した用途 |
|---|---|---|
| オイラー図(Euler Diagram) | 実際の包含関係のみを示す | 集合関係の厳密な表現 |
| UpSet Plot | 集合間の重なりを棒グラフ形式で表示 | 多集合データ分析 |
| ネットワーク図 | 関係性をノードとリンクで表現 | 構造的な依存関係の可視化 |
ベン図とオイラー図の違い
| 項目 | ベン図 | オイラー図 |
|---|---|---|
| 発案者 | ジョン・ベン(1880) | レオンハルト・オイラー(18世紀) |
| 表現対象 | すべての論理的可能性を網羅 | 実際に存在する関係のみを表す |
| 領域数 | (2^n)(nは集合数) | 必要な領域のみ |
| 用途 | 論理・集合論の教育、理論的解析 | 実際の関係図示や概念分類 |
| 図形の形 | 通常は円または閉曲線 | 任意の形(しばしば非対称) |
このように、ベン図は理論的厳密性を優先するのに対し、オイラー図は現実的な関係を簡潔に表現するために使われます。
まとめ
ベン図は、複数の集合や概念の関係を 論理的かつ直感的に表すための基礎的図法 であり、数学・教育・デザインなど多くの分野で重宝されています。
その単純な形の背後には、「論理の全可能性を包含する」という厳密な理念があり、オイラー図との対比を理解することで、より深い洞察を得ることができます。