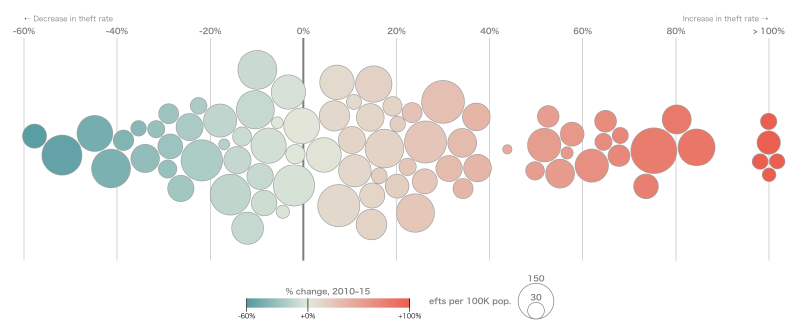
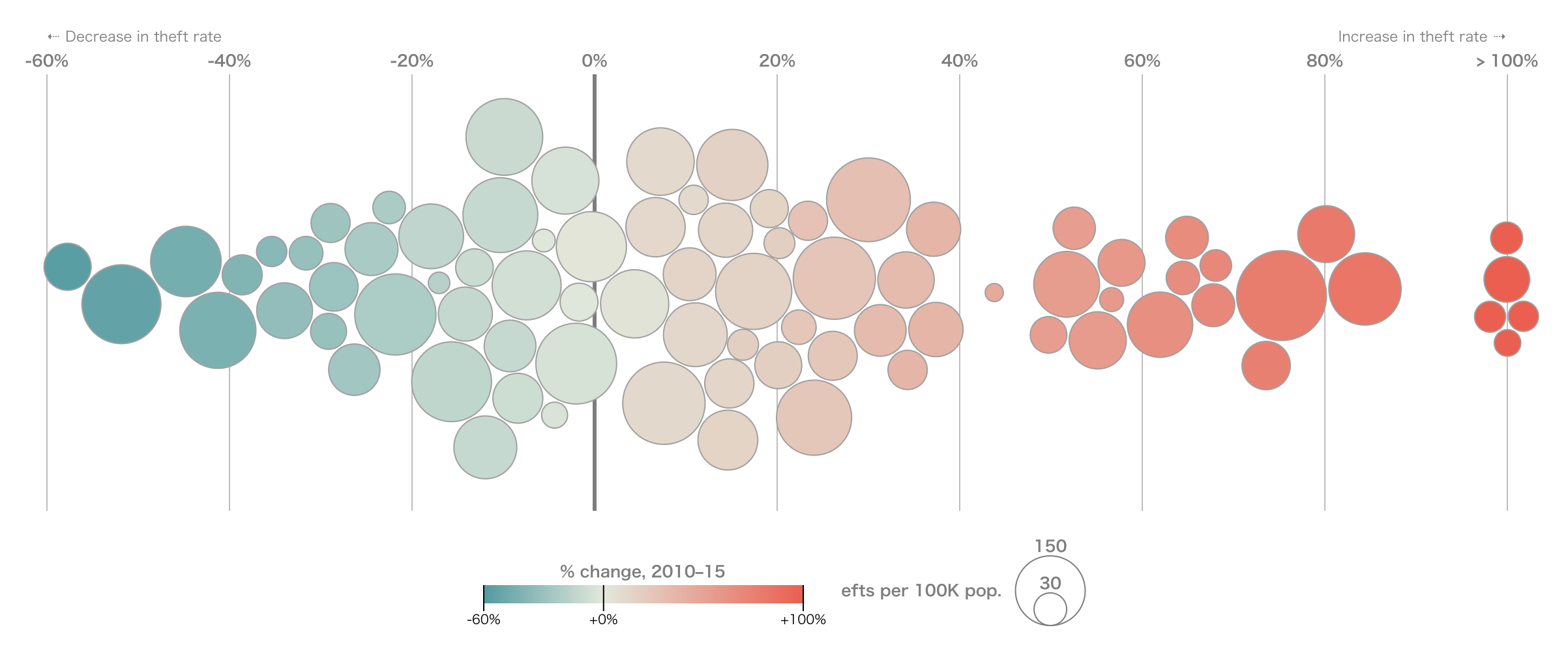
ビースウォーム・プロット(Beeswarm Plot)は、個々のデータ点を重ならないように配置し、データの分布を視覚的に示すチャートです。散布図とバイオリンプロットやボックスプロットの中間的な存在であり、数値変数の分布や密度を「個々の観測値」を保ったまま表現できる点が特徴です。
「Beeswarm(蜂の群れ)」という名の通り、データ点が群れのように並ぶことからこの名前が付けられました。
歴史的経緯
ビースウォーム・プロットは1990年代にR言語のbeeswarmパッケージで一般化されました。以降、Pythonのseaborn.swarmplot()やplotly.express.strip()など、多くのデータ可視化ライブラリで採用されています。
従来のボックスプロットやバイオリンプロットが統計的要約を中心にしていたのに対し、ビースウォームは「個々のデータ点を見せる」トレンドを反映した可視化手法といえます。
データ構造
ビースウォーム・プロットは、主に以下のような構造のデータを扱います。
| 変数名 | 内容 | 型 |
|---|---|---|
| category | 比較したいグループ | 文字列 |
| value | 数値データ | 数値 |
単一カテゴリ内での数値分布を表示することも、複数カテゴリ間での比較を行うことも可能です。
目的
データの個々の分布を詳細に可視化し、統計的要約では見落とされる外れ値やクラスタを確認することが目的です。
とくにサンプル数が中規模(数十〜数百)程度の場合、各データ点をすべて描くことが有効です。
ユースケース
実験データや観測データの群間比較(例:医療研究での群ごとの測定値)
教育・社会調査などでのスコア分布の可視化
ボックスプロットの補完としての使用(統計量に加えて個々の値を示す)
統計可視化 :箱ひげ図やバイオリン図と組み合わせ、要約統計と生データを両立。
機械学習の解釈(SHAP) n:特徴量の重要度を視覚化する際に beeswarm プロットが使われ、個々の観測の影響度を直感的に理解できます。
教育・プレゼン :点が「生きている」ように散らばるため、聴衆に分布の雰囲気を伝えるのに効果的。
特徴
- データの「密集度」を位置によって暗黙的に表現
- 外れ値を自然に表示できる
- 視覚的な「ノイズ」も含めてデータ全体像を捉えられる
- 大規模データには不向き(点の重なりや計算コストが増大)
メリット
- すべての点が見える :要約統計だけでなく、外れ値や個々の観測をそのまま確認可能。
- 分布の偏りが直感的 :点の群れ具合から、密集やばらつきがすぐに分かる。
- 比較がしやすい :カテゴリごとに並べることで、グループ間の分布差を直接見比べられる。
注意点
- 大量データには不向き :数万件単位のデータでは処理も表示も重くなる。
- 「幅」に定量性はない :横方向の広がりは単なる重なり回避であり、密度を厳密に測るものではない。
- 視覚的調整が必要 :パラメータ設定を工夫しないと点が雑然として見えることがある。
チャートの見方
- 基本構造 …縦軸(あるいは横軸)に数値データを、横軸(あるいは縦軸)にカテゴリ変数を配置します。
- 重なりの解消 …単純なストリッププロット(strip plot)では点が重なってしまいますが、ビースウォームではアルゴリズムによって点をずらし、衝突しないように散らします。
- 配置の意味 …数値軸方向はデータ値を保持し、カテゴリ軸方向には重なりを避けるための調整だけが行われます。そのため、点が横に広がるほど「その数値付近に多くの観測がある」ことを意味します。
デザイン上の注意点
- サンプルサイズが大きすぎると過密化:ランダムサンプリングや透明度の調整を検討します。
- 点の大きさと間隔の調整:プロットの「蜂の群れ」感を損なわないように調整します。
- カテゴリ数が多い場合は視認性が低下:グループ数は控えめに。
- 軸ラベルや注釈を明確にして、数値スケールを理解しやすくします。
応用例
- ボックスプロット+ビースウォームの重ね合わせ(Seabornの
swarmplotとboxplotの併用) - **ストリッププロット(Strip Plot)**との比較:ストリッププロットは重なりを避けない単純散布。
- バイオリンプロットとの併用で、統計的要約+個別点の両立。
代替例
| チャート名 | 概要 | 適用条件 |
|---|---|---|
| ボックスプロット | 四分位範囲と外れ値を統計的に表現 | サンプル数が多い場合 |
| バイオリンプロット | 分布の密度形状を滑らかに表示 | データが連続分布に近い場合 |
| ストリッププロット | データ点を単純に並べる | 小規模データで簡易表示したい場合 |
まとめ
ビースウォーム・プロットは、データの「個別性」と「分布性」を同時に示せる可視化手法です。適切なデータサイズで用いれば、他のチャートでは見えにくい外れ値や集中度を明快に伝えることができます。