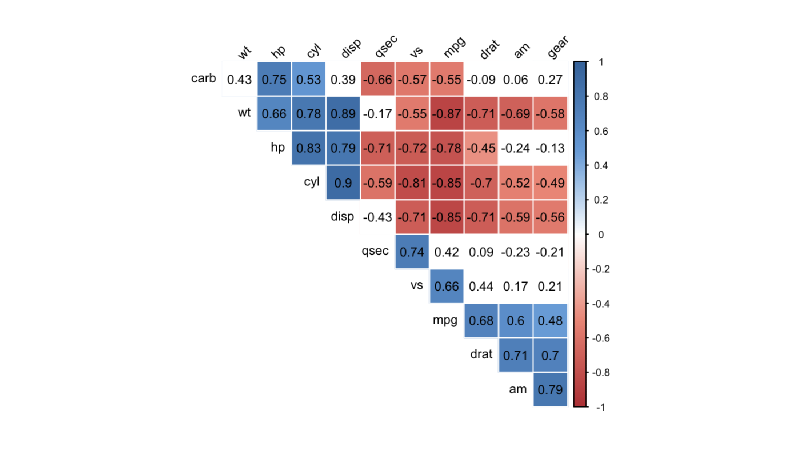
コレログラム(Correlogram)は 複数の変数間の相関関係を行列形式で可視化するチャート です。縦軸・横軸に変数を配置し、それぞれの交点において 相関係数(correlation coefficient) を色や形で表現します。データの相関構造を俯瞰的に把握でき 強い正の相関・負の相関・無相関 を一目で判別できます。散布図行列のように「関係の方向性」ではなく「関係の強さ」に焦点を当てる点が特徴です。
歴史的経緯
コレログラムという用語自体は統計学で古くから存在し、もともとは時系列データの自己相関(autocorrelation)をプロットする図を指していました。しかし多変量解析や可視化の文脈では、相関行列の視覚化手法として再定義され、広く使われるようになりました。
R言語の可視化パッケージである corrplot(Taiyun Wei, 2013) が普及のきっかけとなり、Pythonでも Seaborn や Matplotlib を通じて類似表現が標準化しました。現在ではデータ分析の初期段階における 探索的データ分析(EDA) の定番手法となっています。
データ構造
コレログラムは 相関行列(correlation matrix) を入力データとして用います。一般的には、数値データの各変数間のピアソン相関係数を計算して構成されます。
| フィールド | 内容 |
|---|---|
| 変数A | 行方向の変数 |
| 変数B | 列方向の変数 |
| 相関係数 r | -1.0〜+1.0 の実数値(正負の強度を示す) |
例(Pythonコード):
| |
目的
コレログラムの主な目的は、変数間の関係性を全体として把握することです。 どの変数が似た傾向を持つか、逆の動きをするかを視覚的に確認でき、多変量間の相関構造を一目で理解するための探索的ツールとして用いられます。
- 特徴量間の関係確認:多重共線性(multicollinearity)の検出
- クラスタリング前の探索分析:似た傾向を持つ変数のグルーピング
- データ前処理の判断:変数削除・縮約の判断材料
- EDA (探索的データ解析):全体的な関係構造の理解
ユースケース
- 統計分析や機械学習の前処理における特徴量選定
- 経済指標・株価データなどの変動関係の分析
- 医療データや心理測定データの変数相関の評価
- 顧客行動データの特徴分析(マーケティング分析など)
特徴
| 観点 | 内容 |
|---|---|
| 表現形式 | 行列形式(変数×変数) |
| 視覚符号 | 色・形・大きさで相関係数を表現 |
| 値の範囲 | -1(完全負)〜 +1(完全正) |
| 主な使用変数 | 数値型変数 |
| 対称性 | 行列は対称(変数A–BとB–Aは同一) |
| 長所 | 多数の変数の関係を俯瞰できる/正負の関係が一目でわかる |
| 短所 | 非線形関係や外れ値の影響を表しにくい/変数が多いと判読性が低下する |
| 推奨カラーマップ | 中立点(0)を中心とした連続配色(例:coolwarm, RdBu) |
| 主な使用場面 | 探索的データ分析(EDA)/特徴量選定/データ相関の全体像把握 |
チャートの見方
コレログラムの構造は以下のようになっています。
| 要素 | 内容 | 解釈のポイント |
|---|---|---|
| 行・列 | 変数の一覧 | それぞれの組み合わせごとに相関を示す |
| セルの色 | 相関係数の符号と強さ(例:青=正、赤=負) | 相関の方向と大きさを視覚的に判断 |
| 色の濃さ・円の大きさ | 相関の絶対値(強弱) | 強い関係ほど濃く・大きく表示される |
| 対角線上 | 各変数自身(相関=1) | 通常は空白、または1.0と表示される |
| 数値ラベル(任意) | 相関係数の実数値 | 精度を確認したい場合に併記される |
このように、コレログラムは 相関の方向(正負)と強さ を瞬時に読み取れる設計になっています。視覚的なパターンから、似た傾向を持つ変数群を特定することが可能です。
左右対称な行列構造のため、上三角・下三角のどちらかのみを表示する簡略版も一般的です。
デザイン上の注意点
- カラーマップは連続値の中立点(0)を中心に対称的に設定する(例:coolwarm)。
- 相関係数の大小を強調するために彩度コントラストを確保する。
- 変数数が多い場合は、相関が強いペアのみを抽出するなどの工夫が必要。
- 外れ値やスケーリングの影響を考慮し、**相関の算出方法(Pearson, Spearmanなど)**を明示する。
コレログラムは「線形相関」のみを対象とすることが多いため、非線形関係を見落とす可能性があります。
また、カテゴリ変数を扱う場合には別途相関係数の選択(Cramér’s V など)が必要です。
さらに、変数数が多いと視覚的に密集し、解釈が難しくなるため、主要変数のみを抽出して表示するのが望ましいです。
応用例
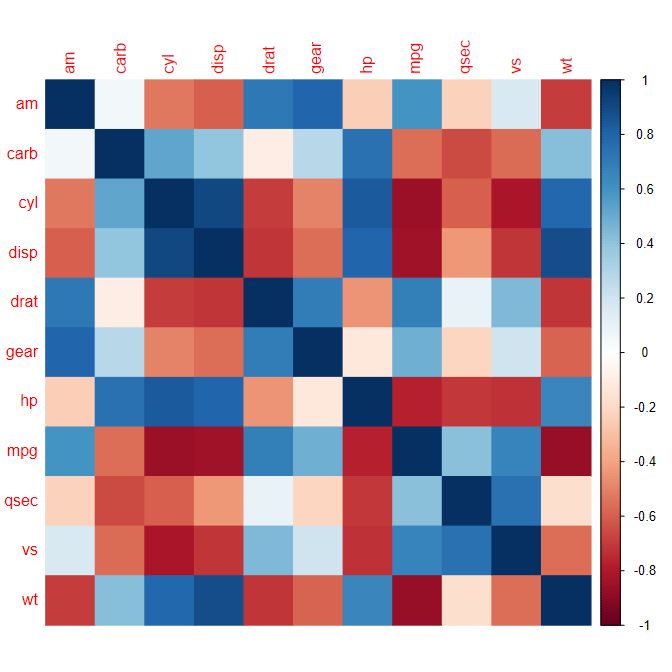
- Seaborn Heatmap:標準的な相関可視化手法。色で相関強度を表現。
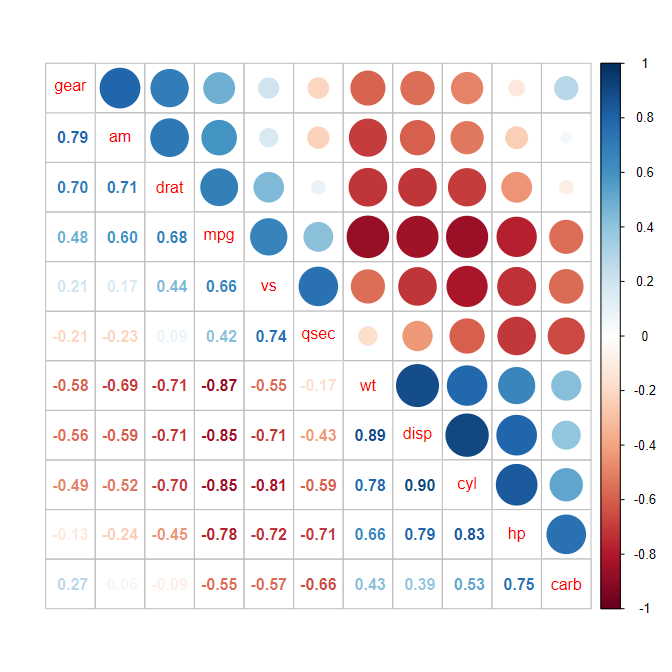
- R corrplot:円の大きさ・色・向きで相関の符号と強度を表現。
- Pairplotとの併用:散布図行列と合わせることで相関の形状を補足。
- 時系列コレログラム:自己相関を時間遅れごとに示す応用例。
代替例
| 手法 | 特徴 | 適する状況 |
|---|---|---|
| 散布図行列(Pairplot) | 各変数ペアの関係を散布図で表示。相関の形(線形・非線形)も確認可能。 | 相関の方向や非線形性を視覚的に確認したい場合 |
| ヒートマップ(Heatmap) | 任意の数値行列を色で表現。相関行列以外の数値比較にも対応。 | 相関以外の値の強弱やパターンを可視化したい場合 |
| ネットワーク図(Correlation Network) | 強い相関を持つ変数同士をノードとエッジで結ぶ。構造的な関係を強調。 | 相関関係を構造として捉えたい場合/クラスター関係を強調したい場合 |
| バブルマトリクス(Bubble Matrix) | セルを円の大きさと色で表す。視覚的に柔らかく理解できる。 | ヒートマップをより装飾的・直感的に見せたい場合 |
| サンキーダイアグラム(Sankey Diagram) | 変数間のフローや関連性を線幅で表現。 | 相関を「流れ」や「結びつき」として説明したい場合 |
まとめ
コレログラムは、多変量データの相関構造を一目で俯瞰できる強力な分析ツールです。特にデータ探索や前処理段階において有効であり、変数間の依存関係や冗長性を理解する助けになります。ただし、相関は因果関係を意味しないため、「関係の強さ」以上を読み取らない慎重さが求められます。