配色の設計 ―色の知覚と相互作用(”Interaction of Color”)
ジョセフ・アルバースさんによる色彩の研究成果をまとめた書籍「配色の設計 ―色の知覚と相互作用(”Interaction of Color”)」は、彼のキャリアの晩年、勤めていたイェール大学から出版されています。
この中で、**「ウェーバー - フェヒナーの法則」(Weber-Fechner Law)**を紹介しています。これは、
「等差数列的な変化を視覚的にとらえるためには、物理的には等比級数的に増えてゆかねばならない」(翻訳書より抜粋)
ことを示した法則です。等差数列と等比数列を補足します。
- 等差数列(Arithmetical progression)…「はじめの数に、一定の数を足し算し続けて、その結果出来た数列」
- 等比数列(Geometric progression)…「はじめの数に、一定の数を掛け算し続けて、その結果出来た数列」
書籍中では、1.白い紙の上で、薄い黄色を塗り重ねていった場合、2.赤に黒を段階的に足していった場合の二例について、実際の結果が掲載されています。
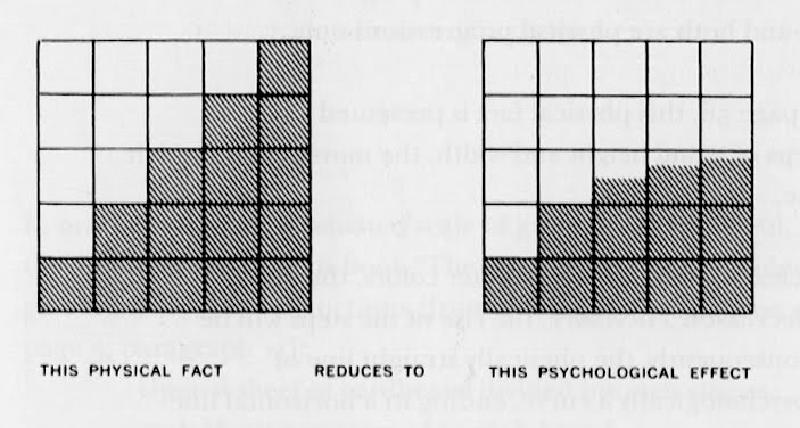
これを概念的に示しているのが下の二画像です。横軸が時系列(重ね塗りした回数)になり、縦軸は少しややこしいですが左図がの場合は物理的事実、右図の場合は心理的効果の大きさ、という解釈になるかと思います。

等差数列(arithmetical progression)で物理的に描かれたもの(左)は、過小評価、実際よりも削減されて知覚される(右)。

等比数列(Geometric progression)で物理的に描く(左)ことで、やっと等差数列(arithmetical progression)のように知覚される(右)。
実際の色の変化と、人間の知覚が、線形(等差数列)ではないことを示しています。
ジョセフ・アルバースさんによるこの書籍(配色の設計 ―色の知覚と相互作用)は1963年の出版。
参照している「ウェーバー - フェヒナーの法則」(Weber-Fechner Law)は1860年の初出。
近い内容を示す、「スティーヴンスのべき法則」(Stevens’ Power Law) は1975年の論文であり、「ウェーバー - フェヒナーの法則」よりもずっとあと、この書籍よりも少し後のことでした。